Výběr z textů

MAREK VESELÝ
Fyzikální úloha Sherlocka Holmese

Člověk by se ani nenadál, že v beletrii jsou ukryty fyzikální úlohy. Jednu takovou jsem objevil v povídce Stříbrný Lysáček od sira Arthura Conana Doyla.

Vypráví doktor Watson...

A tak se stalo, že jsem asi za hodinu seděl v rohu kupé, ve vagóně první třídy, uhánějícím do Exeteru, zatímco Sherlock Holmes, jehož ostře řezavou, dychtivou tvář vroubila cestovní čapka s klapkami na uši, se zahloubal do hromady čerstvých novin, které si opatřil na Paddingtonském nádraží. Byli jsme už daleko za Readingem, když hodil poslední noviny pod lavici a nabídl mi doutník.
"Jede to dobře," řekl, vyhlížeje z okna a zároveň pokukuje po hodinkách. "V této chvíli máme rychlost třiapadesát a půl míle v hodině."
"Nedával jsem pozor na milníky," řekl jsem.
"To já také ne. Telegrafní sloupy jsou však na této trati od sebe vzdáleny šedesát yardů, a tak je snadné to vypočítat. Předpokládám, že jste se už poněkud obeznámil s tou vraždou Johna Strakera a se zmizením Stříbrného Lysáčka?"

Tolik tedy autor detektivky, a teď už nastupuje fantazie a vynalézavost učitele fyziky. Pro inspiraci uvádím několik otázek, které můžete žákům předložit k řešení. Já věřím, že Vy přijdete ještě na jiné, lepší.

1. Jaká je vzdálenost mezi telegrafními sloupy v metrech?
2. Jaká byla rychlost vlaku v kilometrech za hodinu?
3. Převeďte rychlost v mílích za hodinu na yardy za sekundu.
4. Jakým způsobem vlastně Sherlock Holmes vypočetl rychlost vlaku?
5. Jak dlouho Sherlock Holmes vykukoval z okna, když minuli celkem 13 telegrafních mezer?

Převodní vztahy mezi jednotkami:

yard - 1 yd = 0,9144 m (přesně)

míle - 1 mile = 1609,344 m (přesně)

1 mile = 1760 yd

Literatura:

1. Doyle, A. C.: Muž s dýmkou a houslemi. Praha, Albatros 1987

2. Matematické, fyzikální a chemické tabulky pro střední školy. Praha, SPN 1983

Řešení:

1. 54,84 m

2. 86,1 km/h

3. 26,2 yd/s

4. v=s/t

5. 30 s - výsledky jsou zaokrouhleny

Dodatek D.S.:

Bravo, Watsone! Srdce mi jen plesá, oči holmesologa září svatým nadšením. Sice výše uvedený článek určitě nebyl míněn jako holmesologický, ale do této kategorie bezesporu patří. Jen se bojím, zda se tak v žácích nevypěstuje spíš odpor k Holmesovi, než aby se vzbudil jejich zájem...
O této úloze už bylo také popsáno mnoho papíru a to i největšími kapacitami. Co praví například komentář z The Annotaded Sherlock Holmes od Baring-Goulda? Zde můj neumělý překlad:

"Mnozí pochybují, že by vlak mohl jet takovou rychlostí, ale Mr. Hook upozorňuje, že tato rychlost byla "nejen možná, ale i nutná. Jak Létající Holanďan, tak Zulu potřebovali na cestu z Paddingtonu do Swindownu 87 minut ... Což představuje od výjezdu do zastavení průměrnou rychlost 531 m/h a je zřejmé, že nejvyšší rychlost, aby se dodržela rychlost průměrná, musela být podstatně vyšší než zmíněných 531 m/h."
Mr. A. D. Galbraith shledává ve svém Skutečném Moriartym takový výrok "naprosto neslučitelný s Holmsovou povahou. Holmes byl vždy popisován jako muž přesného uvažování, jako chladný, čistý myslitel. Musel by tedy svým výrokem myslet, že jeho výpočet rychlosti není nepřesný o více, než o čtvrt míle za hodinu; tzn. že třiapadesát a půl míle za hodinu je nejblížší zaokrouhlení na celou půlmíli. On ale stopoval čas na obyčejných hodinkách a po poměrně krátkou dobu – Watsonova formulace zní "pokukoval po hodinkách" a nemůžeme očekávat, že by vlak udržel stejnou rychlost po více jak dvě minuty. Musel tedy určit z vteřinové ručičky svých hodinek čas od projetí kolem jednoho telegrafního sloupu k jinému, vzdálenému pravděpodobně míli nebo o něco víc, a zároveň počítat mezery mezi sloupy. Každý, kdo to zkusil, ví, že nepřesnost jedné sekundy je na tuto dobu neuvěřitelně malá, dvouvtřinová chyba je ještě přijatelná. Nepřesnost jedné sekundy během dvou minut znamená při této rychlosti chybu skoro poloviny míle na hodinu. Muž přesného vyjadřování, i kdyby byl obdařen nadlidskou přesností v měření času, by tedy řekl "mezi třiapadesáti a čtyřiapadesáti mílemi za hodinu," a ještě rozumnější by byl výrok "mezi dvaapadesáti a pětapadesáti". Pokouší se Holmes ohromit Watsona nebo se pokouší Watson ohromit svého čtenáře?"
Zesnulý profesor Jay Finley Christ analyzuje problém v článku Sherlock jede rychlíkem a dochází k závěru, že výpočet nebyl snadný; Mr. Guy Warrack zastává ve své knize Sherlock Holmes a hudba názor, že aby se Holmes dostal k danému výsledku, musel by z hlavy spočítat ohromně složitý výsledek, a že by bylo nemožné s kapesními hodinkami odměřit čas na potřebnou desetinu sekundy. Mr. S. C. Roberts ve své recenzi knihy Mr. Warracka Hudba v Baker Street ale namítá: "Mr. Warrack, smíme-li to tak říci, dokazuje své telegrafní sloupy plnicím perem. Co se jistě přihodilo, bylo zhruba toto: Asi půl minuty před tím než oslovil Watsona, Holmes sledoval vteřinovou ručičku svých hodinek a odpočítal patnáct telegrafních sloupů (Musel samozřejmě vidět milníky, ale nevšímal si jich, protože tyto neslouží za základ jeho výpočtu.) Tím získal vzdálenost 900 yardů, více než půl míle. Kdyby mu sledování vteřinové ručičky prozradilo, že uplynulo třicet sekund, věděl by hned, že vlak jede zhruba rychlostí šedesát mil za hodinu. Ve skutečnosti si všiml, že vlak potřeboval na oněch 900 yardů zhruba 34 sekund; jinými slovy o něco více než deset procent (tedy 61 ze 60). Výpočet je, jak říká, jednoduchý. Co jej dělá jednoduchý, je jeho vědomost, kterou s ním samozřejmě Watson nesdílí, že telegrafní sloupy jsou od sebe vzáleny 60 yardů. Řeč Mr. Warracka o "vyloženém blufu" je zjevně irrelevantní."
Mr. George W. Welch navrhuje ve Vzorci Stříbrného Lysáčka ne jeden, ale hned dva vzorce, které jsou údajně jednoduché:

První metoda: –Vezměme dvě sekundy na každý yard a připočtěme další sekundu na každých 22 yardů známé vzdálenosti. Pak počet objektů, které mineme v tomto čase je rychlost v mílích za hodinu. Zkouška: –X = rychlost v mílích za hodinu, y = vzdálenost mezi sousedními objekty. 1 m/h = 1.760 yardů za 3.600 sekund = 1 yard za 3.600/1.760 sekund (= 45/22 nebo 2 1/22 sec.) = y yardů za 2 1/22 sekund x m/h = xy yardů za 2 1/22 sekund. Příklad: –Telegrafní sloupy jsou od sebe vzdáleny 60 yardů. 60 * 2 = 120; 60 / 22 = 3 (zaokrouhleno); 120 + 3 = 123. Takže, pokud je za 123 sekund pozorovatel mezi 53. a 54. sloupem, je rychlost vlaku 531 míle za hodinu.
Druhá metoda: –Pokud čas nebo trasa nedovolí použít první metodu, vezmeme jednu sekundu pro každý yard známé vzdálenosti a znásobíme 2 1/22 počet objektů, které jsme v daném čase minuli. Výsledek je rychlost v mílích za hodinu. Příklad: –Telegrafní sloupy jsou od sebe vzdáleny 60 yardů. Po 60 sekundách je pozorovatel zhruba 10 yardů za 26. sloupem. 26 1/6 * 2 = 52 1/3; 26 1/6 děleno 22 = zhruba 1 1/6; 52 1/3 + 1 1/6 = 531. Tedy rychlost vlaku je 531 míle za hodinu. Výhodou první metody je, že potřebný čas může být vypočítán předem a pozorovatel nemusí dělat nic jiného, než počítat předměty a sledovat daný čas na hodinkách.

"Teď ale," píše dr. Julian Wolff v Dynamice binomického teorému, "se podívejme na problém ve světle čistého přemýšlení. Za prvé, rychlost ve stopách za sekundu se dá snadno zjistit odměřením počtu sekund potřebných ke zdolání trasy o známém počtu stop. Tedy rychlost při míjení  deseti mezer mezi telegrafními sloupy (1.800 stop, neboť Holmes praví, že sloupy jsou od sebe vzdáleny 60 yardů) za T sekund je 1800/T stop za sekundu. Znásobením tototo čísla 3600 dostaneme rychlost ve stopách za hodinu, a vydělením výsledku 5280 dostaneme rychlost v mílích za hodinu. Tedy:

míle za hodinu = ( 1800 * 3600 / T ) / 5280 = 1227,27 / T

Jinými slovy, všechno, co musíme udělat, abychom zjistili rychlost vlaku v mílích za hodinu, je vydělit 1227,27 (1227 je už dostatečně přesné pro všechny obyčejné účely, jako např. ohromit Watsona) počtem sekund potřebných ke zdolání trasy dlouhé 1800 stop. Pro všechny, kteří nezvládnou tak jednoduchý výpočet, připojujeme graf."

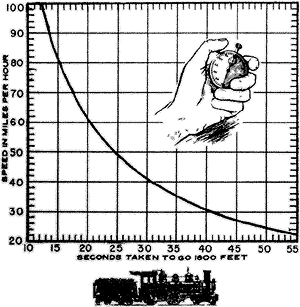
The Annotated Sherlock Holmes II, p. 262 f.